前言

對圖形的搜尋有了基本觀念之後，接下來要在圖形的邊加入權重的部分，這樣就能找到最短路徑

生活常識

你有自己規劃行程的經驗嗎？如果朋友住在台中住在想去花蓮旅遊，那麼你會怎麼建議行程呢？是建議從南投走橫貫公路，還是從繞到台北宜蘭，還是打開 googe map 直接看哪個路徑比較短，或是花費的時間比較少，由下圖可以看到 google map 推薦路程時間最少的(走往台北的路徑)，而不是距離最短的路徑(走往南投的路徑)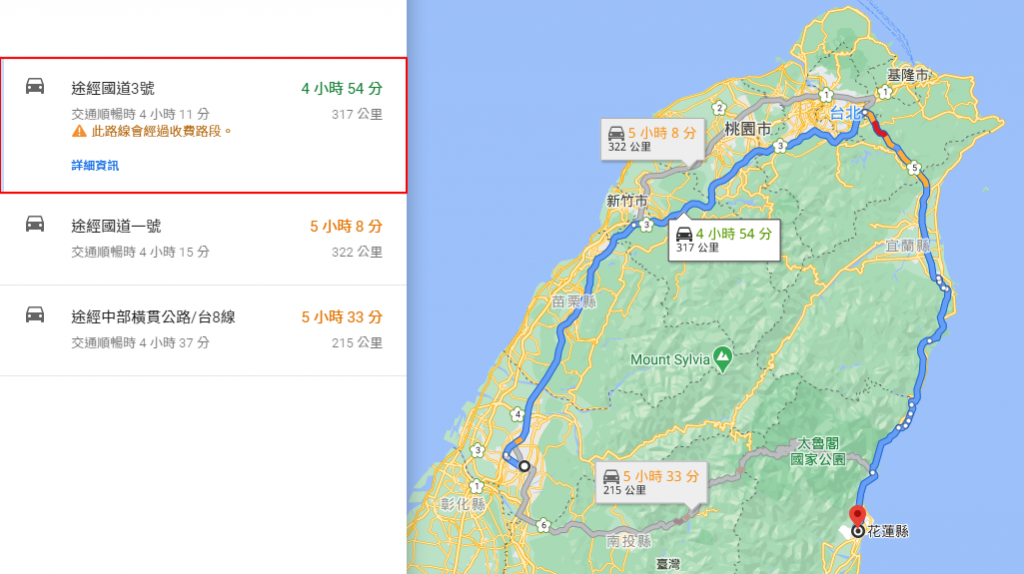

專業知識 - 戴克斯特拉演算法 Dijkstra's algorithm

戴克斯特拉演算法因為音譯的關係有蠻多種說法的，每一種名字都蠻常的XD，我自己是比較習慣用英文記憶XD，回歸正題，如果僅以邊作為挑選路徑的考量，也就是圖形中 A 點到 B 點經過幾個邊，可以使用昨天介紹的廣度或深度演算法，但如果加上時間的考量，則廣度搜尋演算法的結果並不一定會等於戴克斯特拉演算法的結果

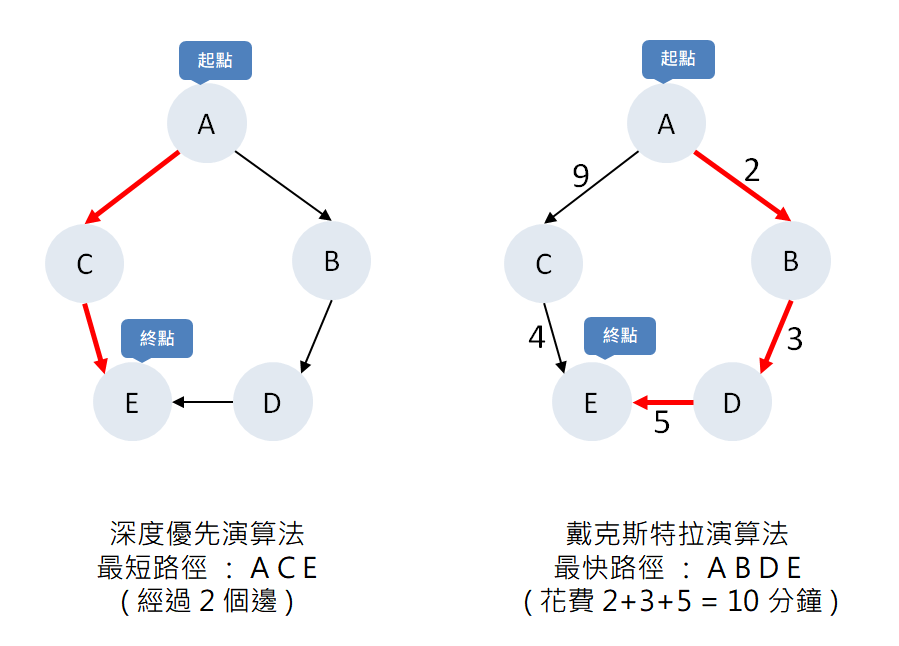
如下圖，起點為 A 點，目的地為 E 點：

• 左圖
  沒有時間的權重，所以最短路徑會選 ACE，此路段最少，因為只需要經過2個邊

• 右圖
  加上時間的權重，單位為分鐘，ACE 花費時間為 13(9+4) 分鐘，雖然 ABDE 要走 3 個邊但只需要花 10 分鐘，所以走 ABDE 最快

最短路徑 Single-Pair Shortest Path

有一個有向加權圖形 G = ( V, E )，最短路徑為圖中兩頂點間的最短路徑，也就是權重加總數值最小者，其中加權的部分，就看個人的考量，也許是時間，或是開車油錢等等

例子

以下圖為例，權重為公里，想要找到 A 到任一點最短的路徑，透過戴克斯特拉演算法要如何取得結果，這邊要特別注意，使用戴克斯特拉演算法時，圖形中的權重不能有負數(正負數)，否則演算法的結果可能會有錯誤，須改用其他演算法，像是貝爾曼福特演算法(Bellman-Ford algorithm)

先來看搜尋結果，稍後會有詳細的步驟說明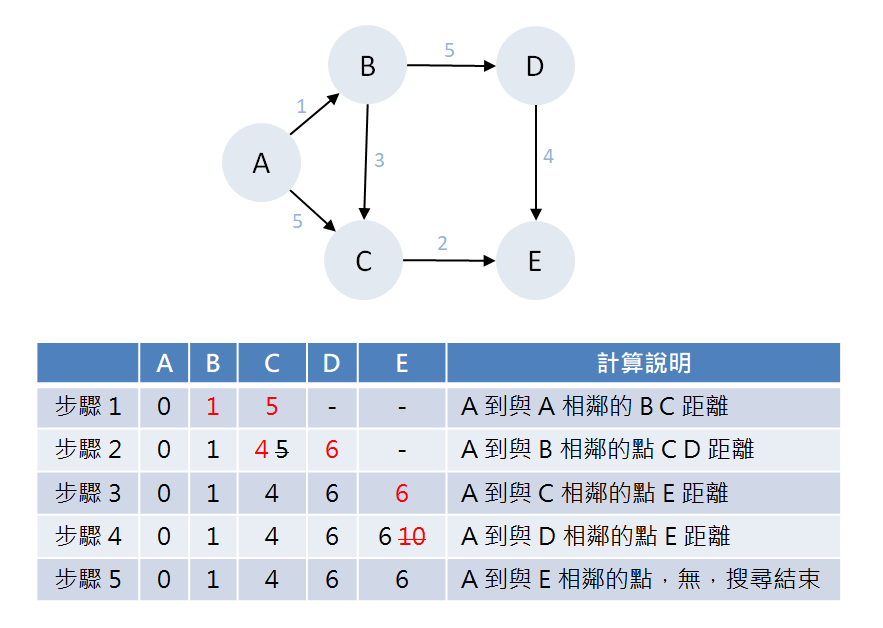

可由步驟 5 觀察到，A 到任一點的最短距離
A 到 A 的最短距離為 0
A 到 B 的最短距離為 1
A 到 C 的最短距離為 4
A 到 D 的最短距離為 6
A 到 E 的最短距離為 6

步驟說明：

1. 尋找與 A 到相鄰的點 B 與 C 的最短路徑
   A 到 B 點：1 公里
   A 到 C 點：5 公里
   此時不知道 D 與 E 距離 A 多遠，所以先畫 - 符號表示無窮大

2. 尋找與 B 到相鄰的點 C 與 D 的最短路徑
   A 到 C 點：上個步驟的 A 到 C 是 5 公里，但 A 經過 B 在到 C 的距離更短，只需要 4 公里，所以將 A 到 C 的距離更新為 4
   A 到 D 點：A 到 D 點的距離為 6 = 1( A 到 B ) + 5( B 到 D)，將表格中的 - 符號更新為 6

3. 尋找與 C 到相鄰的點 E 的最短路徑
   A 到 E 點：先查詢表格，A 到 C 的最短距離計算的結果為 4 公里( A 到 B 再到 C)，C 到 E 的距離為 2 公里，所以 A 到 E 的最短距離為 6 ( 2 + 4 ) 公里

4. 尋找與 D 到相鄰的點 E 的最短路徑
   A 到 E 點：先查詢表格，A 到 D 的最短距離為 6 公里，D 到 E 為 4 公里，所以 A 經過 D 再到 E 的路徑為 10 ( 6 + 4 ) 公里，但與第 3 步驟的 A 到 E 中間通過 C 點比較，發現 10 大於 6 ，所以 10 不是最短路徑，不更新表格數值

5. 尋找與 D 到相鄰的點 E 的最短路徑
   E 點沒有相鄰頂點，結束搜尋，如果表格中還含有 - 符號，代表 A 到無法抵達此點

今日小結

執行戴克斯特拉演算法，在計算過程中，我們需要去取得資料並記錄結果，這個過程需要到記憶體空間，也就是如何將這些資料儲存起來，會使用到之前提到的資料結構，你會選擇那些資料結構來搭配這個演算法呢？其實之前的章節都有說過，不訪動動腦想想看哦

今日謎題

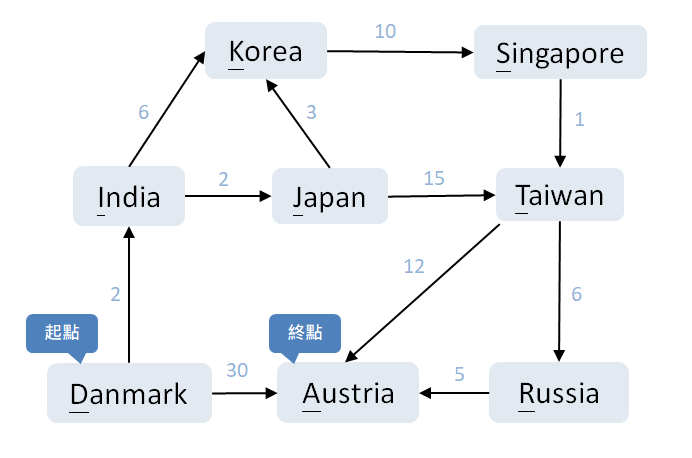
小美要從丹麥(Danmark)到澳洲(Austria)找一個人，下圖是任意門的傳送點與路徑，上面是標注每條路線要走幾公里才能抵達下一個任意門，你可以幫小美找出最短路徑嗎？這條最短路徑似乎按藏著關於小美要找的人的訊息，你能發現嗎？

昨日謎題

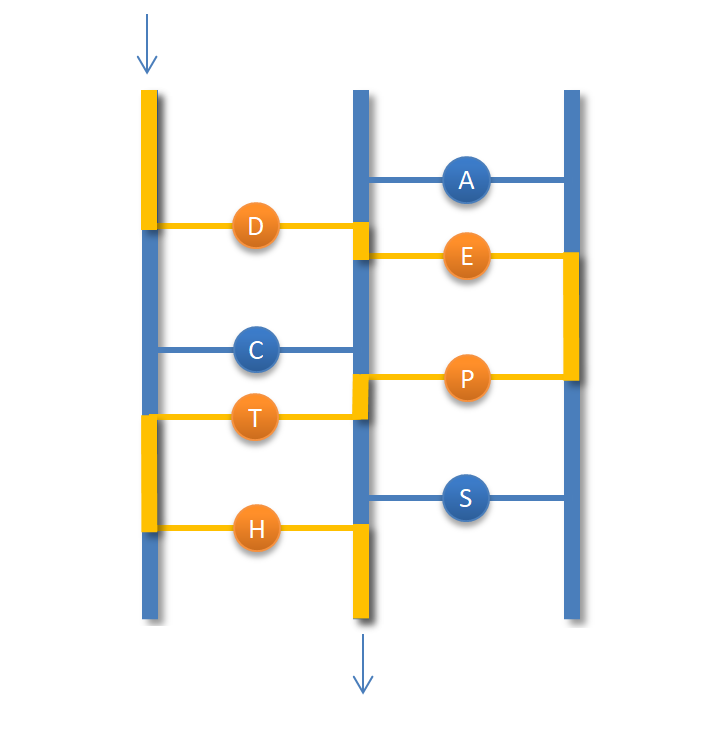
謎題說明：利用走梯子遊戲來感受一下深度優先搜尋，走訪三條路徑之後，可以發現只有第一條可以組成一個有意義的單字，答案就是 DEPTH(深度)，你答對了嗎